Self-Organizing Maps (SOMs) is a method of cluster analysis that are somewhat related to k-means clustering. SOMs were invented in by Teuvo Kohonen in the early 1980s, and have recently been used in genomic analysis (see Chu 1998, Tamayo 1999 and Golub 1999 in references). The Tamayo paper contains a simple explanation of the methods. A more detailed description is available in the book by Kohonen, Self-Organizing Maps, 1997.
The current implementation varies slightly from that of Tamayo et al., in that it restricts the analysis one-dimensional SOMs along each axis, as opposed to a two-dimensional network. The one-dimensional SOM is used to reorder the elements on whichever axes are selected. The result is similar to the result of k-means clustering, except that, unlike in k-means clustering, the nodes in a SOM are ordered. This tends to result in a relatively smooth transition between groups.
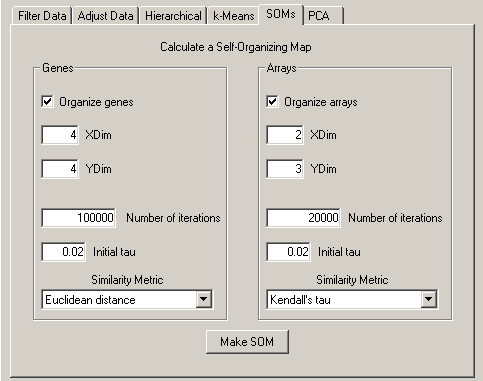
The options for SOMs are
The output file is of the form JobName_SOM_GXg-Yg_AXa-Ya.txt, where GXg-Yg is included if genes were organized, and AXg-Yg is included if arrays were organized. X and Y represent the dimensions of the corresponding SOM. Up to two additional files (.gnf and .anf) are written containing the vectors for the SOM nodes.
In previous versions of Cluster, only one-dimensional SOMs were supported. The current version of the Cluster introduces two-dimensional SOMs.
SOMs and hierarchical clustering: Our original use of SOMs (see Chu et al., 1998) was motivated by the desire to take advantage of the properties of both SOMs and hierarchical clustering. This was accomplished by first computing a one dimensional SOM, and using the ordering from the SOM to guide the flipping of nodes in the hierarchical tree. In Cluster, after a SOM is run on a dataset, the GORDER and/or EORDER fields are set to the ordering from the SOM so that, for subsequent hierarchical clustering runs, the output ordering will come as close as possible to the ordering in the SOM without violating the structure of the tree.